Sólidos arquimedianos Muy interesante

Hecho por: Diego Bonilla

Sólidos arquimedianosLos sólidos arquimedianos o sólidos de Arquímedes son un grupo de poliedros convexos cuyas caras son polígonos regulares de dos o más tipos. Todos los sólidos de Arquímedes son de vértices uniformes. La mayoría de ellos se obtienen truncando los sólidos platónicos. Arquímedes describió ampliamente estos cuerpos en trabajos que fueron desapareciendo, fue sólo en el Renacimiento cuando artistas y matemáticos los redescubrieron.

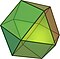
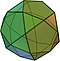
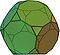
Los sólidos arquimedinos son 13, que se listan a continuación:

Nombre		Imagen	Caras		Aristas	Vértices		Simetría
A1	Tetraedro truncado	Animación	8	4 × hr 4 × te	18	12	12 × 3·6·6	Td
A2	Cuboctaedro	Animación	14	6 × cu 8 × te	24	12	12 × 3·4·3·4	Oh
A3	Cubo truncado	Animación	14	6 × or 8 × te	36	24	24 × 3·8·8	Oh
A4	Octaedro truncado	Animación	14	8 × hr 6 × cu	36	24	24 × 4·6·6	Oh
A5	Rombicuboctaedro o rombicuboctaedro menor	Animación	26	18 × cu 8 × te	48	24	24 × 3·4·4·4	Oh
A6	Cuboctaedro truncado o rombicuboctaedro mayor	Animación	26	6 × or 8 × hr 12 × cu	72	48	48 × 4·6·8	Oh
A7	Cubo romo o cuboctaedro romo (2 formas quirales)	Animación Animación	38	6 × cu 32 × te	60	24	24 × 3·3·3·3·4	O
A8	Icosidodecaedro	Animación	32	12 × pr 20 × te	60	30	30 × 3·5·3·5	Ih
A9	Dodecaedro truncado	Animación	32	12 × dr 20 × te	90	60	60 × 3·10·10	Ih
A10	Icosaedro truncado	Animación	32	20 × hr 12 × pr	90	60	60 × 5·6·6	Ih
A11	Rombicosidodecaedro o rombicosidodecaedro menor	Animación	62	12 × pr 30 × cu 20 × te	120	60	60 × 3·4·5·4	Ih
A12	Icosidodecaedro truncado o rombicosidodecaedro mayor	Animación	62	12 × dr 20 × hr 30 × cu	180	120	120 × 4·6·10	Ih
A13	Dodecaedro romo o icosidodecaedro romo (2 formas quirales)	Animación Animación	92	12 × pr 80 × te	150	60	60 × 3·3·3·3·5	I
dr = decágonos regulares; or = octógonos regulares; hr = hexágonos regulares pr = pentágonos regulares; cu = cuadrados; te = triángulos equiláteros Diego Bonilla